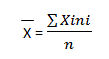Es una distribución de probabilidad que muestra la probabilidad de x ocurrencias de un evento en un intervalo especificado de tiempo o espacio.
Las propiedades de un experimento de Poisson son:
- La probabilidad de una ocurrencia es igual en dos intervalos cualesquiera de igual longitud.
- La ocurrencia o no ocurrencia en cualquier intervalo es independiente de la ocurrencia o no ocurrencia en cualquier otro intervalo.
Se puede usar esta distribución de probabilidad como una aproximación de la distribución binomial cuando p= la probabilidad éxito, es pequeña y n = la cantidad de intentos, es grande.
Tan sólo se iguala a :
La distribución de Poisson se expresa como:
 |
| x = cantidad de ocurrencia. |






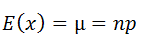










.jpg)
.jpg)
.jpg)
.jpg)
.jpg)


.jpg)









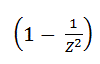




.svg.png)